Problem 47-8    Source:  Problem created by the site's authors.

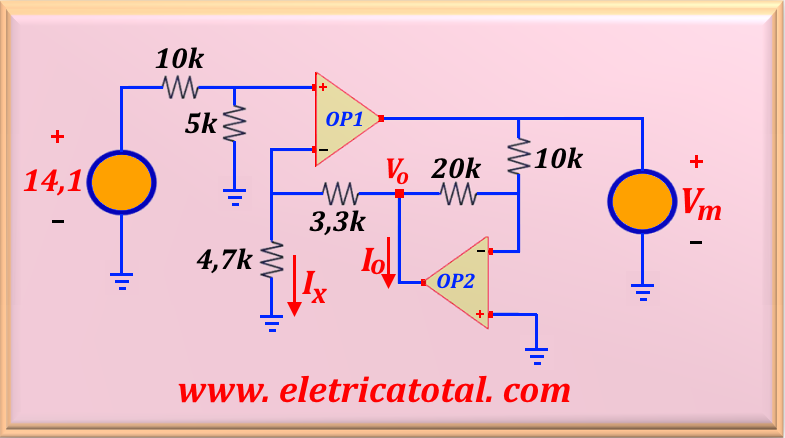
For the circuit shown in Figure 47-8.1, considering V_i = 14.1 V, determine:

a) the value of the current I_x.

b) the voltage value V_o.

c) the voltage value V_m.

d) the value of the current I_o.

Solution of the Problem 47-8   

Item a   

Initially we will determine the voltage at the positive input of the amplifier OP 1.

We must bear in mind that, virtually, the voltage V ⁺ is equal to the voltage at the negative input of the amplifier. Therefore, we know that V ⁺ = V ^- = 4.7 V. With this information we can easily determine the value of I_x, because:

Item b   

Knowing that the current at the input of the operational amplifier is null, we conclude that the current I_x that flows through the 4.7 kΩ resistor also flows through the 3.3 kΩ resistor. This way, we easily find the voltage V_o using Ohm's law, that is:

Item c   

To find the value of V_m we will use the equation eq. 42-01. Thus, after algebraic work, we have:

Item d   

And to calculate the value of I_o, we will apply the nodal method to the output of OP 2, remembering that the voltage at its negative input is the same as that of the positive input, that is, V ⁺ = V ^- = 0 V. Like this:

Replacing with the respective numerical values, we find: