Problema + Difícil 5-2 Fuente:
Problema resuelto por el autor del sitio web.
Usando las transformaciones Delta-Star para el circuito mostrado en la Figura 5-02.1, calcule la resistencia
equivalente entre los puntos a-b
Solução do Problema + Difícil 5.2
Observe que este problema se presenta como elemento principal
un circuito Delta (o triángulo) en paralelo con un circuito estrella (o Y). Pronto, el
primer paso será transformar el circuito estrella en un circuito triángulo.
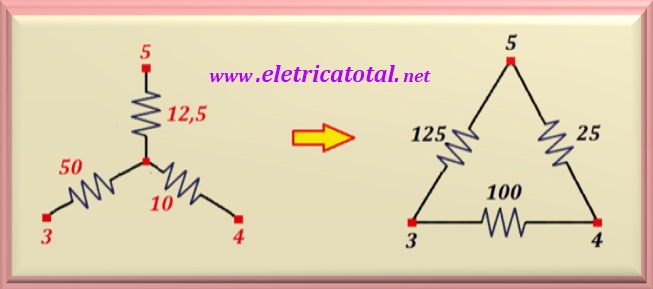
En la Figura 5-02.2 se puede ver la transformación que se debe realizar. Si quieres repasar las ecuaciones
utilizado para llevar a cabo estas transformaciones
clic aquí!
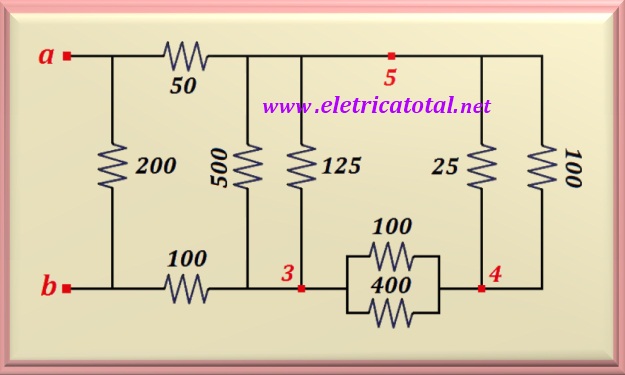
Sustituyendo este nuevo circuito delta en el circuito original, obtenemos la
configuración representada en la Figura 5-02.3, donde se pueden ver los dos circuitos delta en paralelo.
Observe que tenemos un paralelo de tres conjuntos de dos resistencias cada uno.
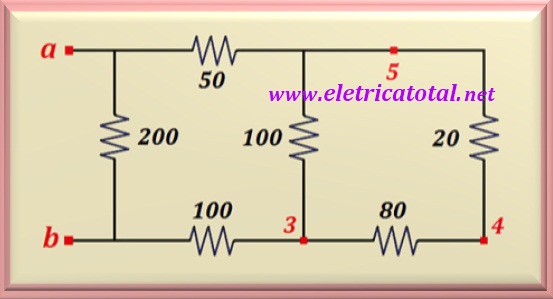
Entonces, resolviendo, nos queda el circuito que se muestra en la Figura 5-02.4.
Tenga en cuenta que entre los puntos 3 y 5 hay dos resistencias en serie:
uno de 20 Ω y el otro de 80 Ω. Sumándolos, obtenemos 100 Ω
para la resistencia equivalente, que
a su vez, está en paralelo con la otra resistencia de 100 Ω. Así,
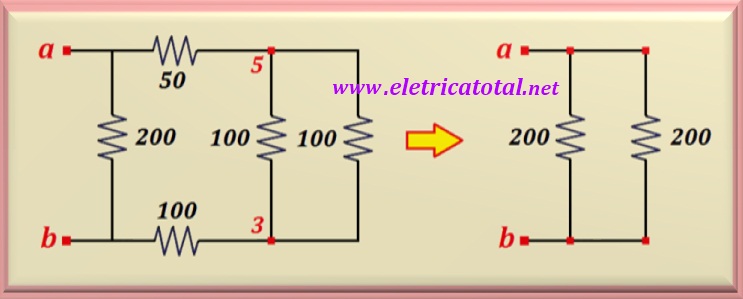
en la Figura 5-02.5, mostramos cómo resultó el circuito.
Así, entre los puntos 3 y 5, con esta asociación aparecen dos resistencias de 100 Ω
cada uno en paralelo, lo que da como resultado una resistencia equivalente de 50 Ω.
Pero esta resistencia equivalente está en serie con las otras dos (una de
50 Ω y los otros 100 Ω), para una resistencia total de 200 Ω.
Finalmente, mirando el lado derecho de la figura, el circuito final que permite
calcular la resistencia equivalente entre los puntos a y b, es decir: