Problem + Hard 55-6    Source:   Problem 33 - List of RLC Problems - Discipline Electrical Circuits of the School of Engineering - UFRGS - 2017 - Prof. doctor Valner Brusamarello.

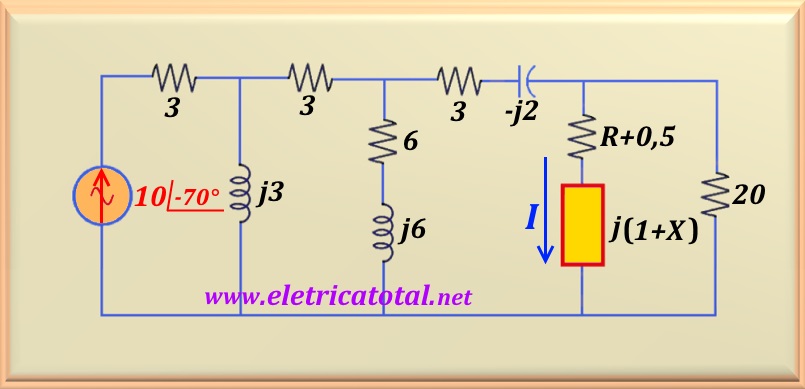
Determine the values ​​of R and X in the circuit of the figure below knowing that I = 1.6∠73.1°.

Attention - In the list of exercises at UFRGS, the answer to this problem has a typo. The correct answer is:   X = -9,  and  R = 1.5. The list contains X = 9. In this case X would be an inductor. It's not the case. X is a capacitor with reactance of 9 ohms, as will be demonstrated in the solution to the problem.

Solution of the Problem + Hard 55-6

The best way to solve this problem is to use the font transformation technique. The resistor of 3 ohms in series with the current source can be eliminated from the circuit without prejudice to the solution. Thus, we can transform the current source in parallel with the inductor of reactance equal to 3 ohms into a 30∠20° voltage source in series with the inductor. This inductor will be in series with the 3 ohm resistor. 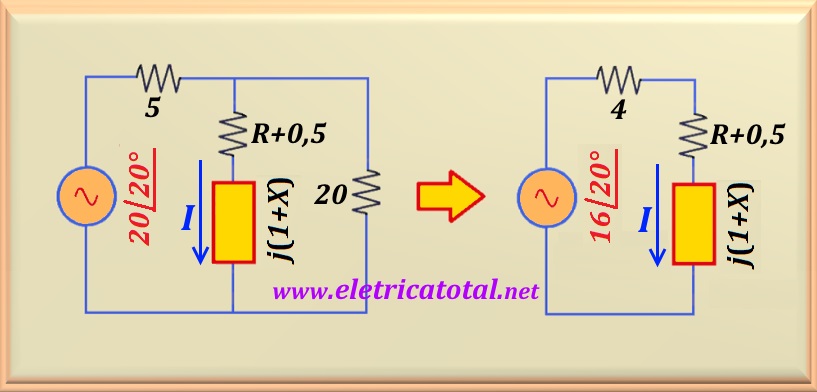Therefore, we can transform this circuit into a new source of current in parallel with this impedance. After some additional transformations we arrive at the circuit shown in the figure below.

Note that in the left circuit we can make one last transformation and arrive at the right circuit. Now, as we know the voltage applied to the circuit and the current flowing through it, the impedance that the circuit offers to the voltage source can be calculated. Then:

On the other hand, the impedance of the circuit is given by:

Then, equating the real part of the last two equations, we find:

Doing the same for the imaginary part, we get:

Therefore, X represents a capacitor with reactance equal to 9 Ω. We must also realize that the current I is leading by 53.1° in relation to the voltage applied to the circuit, This fact is characteristic of a predominantly capacitive circuit.