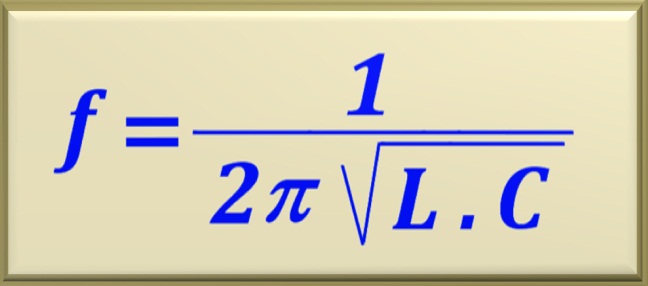Problem 58-1    Source:  Problem elaborated by the author of the site.

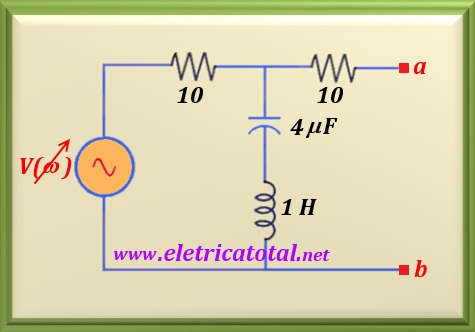
Calculate at what frequency the circuit shown in the Figure 58-1.1 will have the lowest voltage value at the terminals a-b. Make a chart showing the values in around the rejection frequency.

Solution of the Problem 58-1   

This is an LC series circuit. The characteristic of this circuit is that when the capacitive reactance equals the inductive reactance the circuit is at resonance and results in a null impedance between its ends.

Recalling the equation that allows to relate the resonance frequency to the values of the inductor and capacitor.

Thus, substituting the numerical values, we find:

Then, for this frequency X_L = X_C and the resulting impedance will be null. As a consequence, the voltage between the terminals a-b will also be zero. For any other frequency, other than f = 79.58 Hz, there will be in the terminals a-b a voltage other than zero.

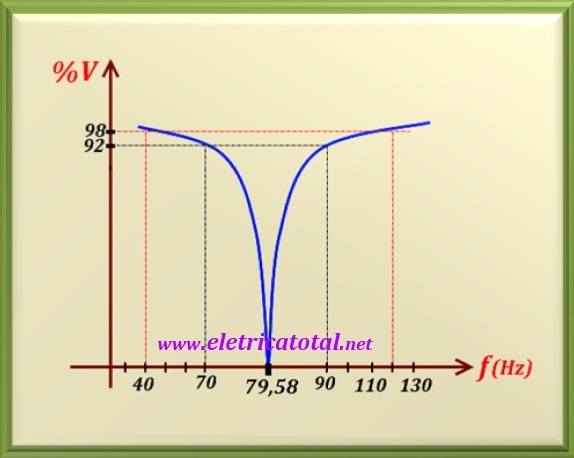
The graph in the Figure 58-1.2 shows how perfect the name of this circuit is, known as the circuit rejects band. Note that at the frequency where X_L = X_C, that is, at the 79.58 Hz frequency, there is no signal at the output. For any other frequency other than this, signal is output. Notice how there is a fall on the output signal as it approaches the rejected frequency. By didactic, no load was placed on the output of the circuit.