Problem 55-22    Source:   Problem elaborated by the site's authors.

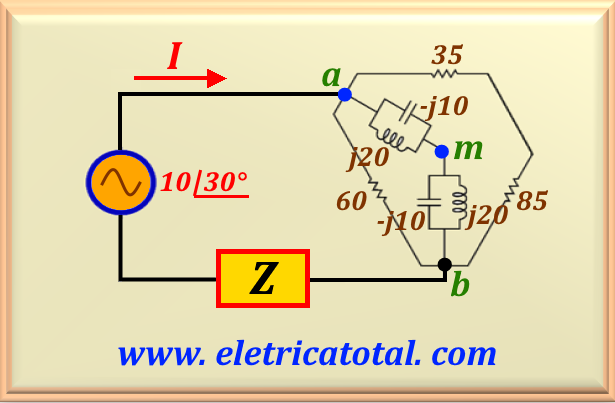
Determine the impedance Z (consider it as load) in the circuit shown in Figure 55-22.1 so that there is maximum power transfer to the load. Find the value of current I.

Solution of the Problem 55-22

To solve this problem we will calculate the impedances between the points a-m and b-m. How do the values of the components are the same so the results will be the same. Calculating the parallel, we obtain

And we know that these reactances are connected in series. Therefore, the equivalent reactance, X_eq, is:

On the other hand, the 35 Ω and 85 Ω resistors are in series. Therefore, it results in a 120 Ω resistor. This resistor is in parallel with the 60 Ω resistor. Calculating the parallel of these resistors we find an equivalent resistor R_eq of:

And since R_eq and X_eq are connected in parallel, solving this parallel we find the equivalent impedance, Z_eq, between points a - b. Soon

We know that for maximum power transfer in the circuit, the impedance value Z must be the complex conjugate of Z_eq. So the value of Z is

Now that we know the value of Z we can calculate the total impedance of the circuit and, thus, find the value of I.

So the value of I is