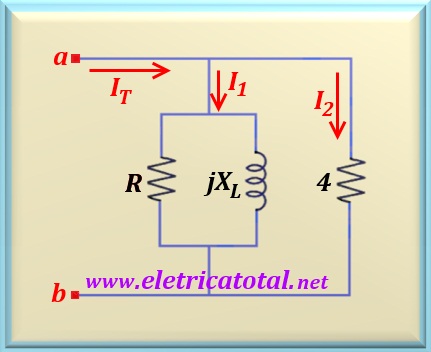
Problem 54-2
Source: Problem 6.7 - page 95 - EDMINISTER, Joseph A. -
Book: Circuitos Elétricos - Ed. McGraw Hill - 1971
The effective values of currents I1 , I2 and
IT are respectively 18 , 15 and 30 A.
Determine the unknown impedances R and XL.
Solution of the Problem 54-2
By doing I2 = 15 ∠0°, we can calculate the value of
Vab. Using Ohm's law:
Applying the Kirchhoff's law to currents in the circuit, we can write:
Note that the parallel formed by R and XL, impedance called
ZL, form a circuit with inductive predominance. With that, we know that
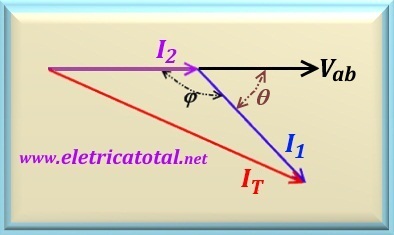
I1 will be late in relation to I2. And as IT
is the phasor sum between I1 e I2, we conclude
that the values of these three phasors form the sides of a triangle, as shown in
the Figure 54-2.2.
As the three sides of the triangle are known, the angle φ can be calculated using the
law of cosines. So:
Making the substitution for the numerical values and making the calculation:
From this data, the angle θ value can be calculated, which is given by:
Note that the convention was used where phasors below the horizontal axis must have negative angles. So, I1 = 18 ∠-49.46°.
We can now calculate the impedance of the parallel circuit, ZL.
On the other hand, we can write the complex admittance for ZL, or:
Therefore, by calculating the inverse of the values we obtain: