Problem + Hard 58-2
Source: Problem elaborated by the website author
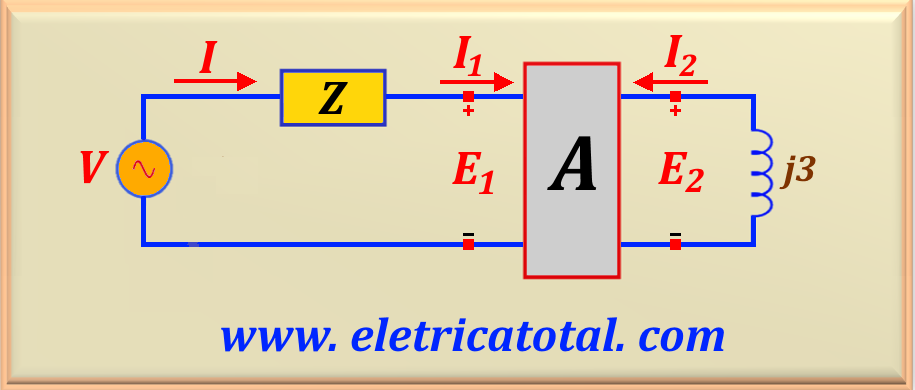
Given the quadrupole equations A below, determine Z so that I is maximum.
Solution of the Problem + Hard 58-2
We must bear in mind that as the problem requires the current I to be maximum, this implies that the circuit must be a series resonant circuit.
In this case, the current I must be equal to I1 in module and sense. Looking at the right side of the quadripole we can write:
This value can be substituted into the equation ⓶. Then:
This equality can be replaced in ⓵, finding:
Note that we found a relationship between E1 and I1, so this allows us to find the equivalent impedance of the circuit to the right of the impedance
Z.
To finalize the solution to the problem, let’s make some considerations. Let's consider Z = R ± j X. For the circuit to be in resonance at
total impedance of the circuit must be a real number. Thus, Z boils down to Z = R - j10. However, as the problem statement requires that the current be maximum,
then R = 0. Therefore: